作为一个非常经典的控制方法,统计过程控制SPC在质量界享誉百年。但在很多企业应用过程中,由于对SPC的理解不足,使用不当,根本没有发挥它的价值。
SPC的概念:
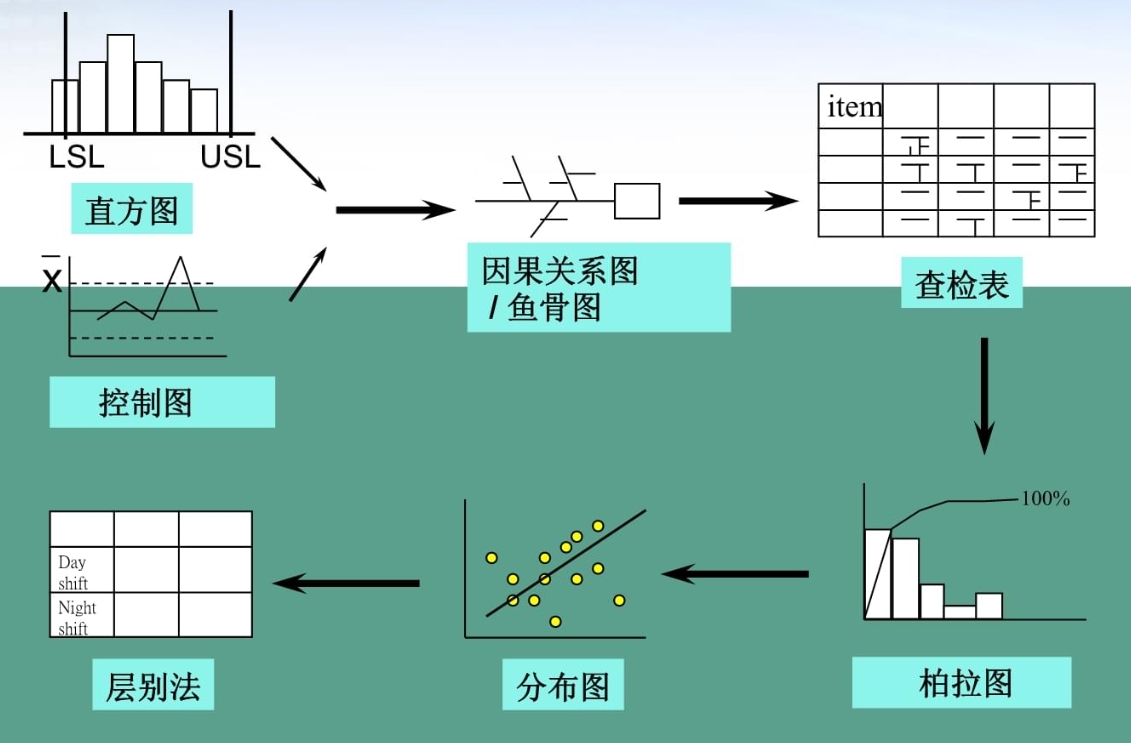
广义的SPC包括传统的7大质量工具(the magnificent seven):
1) Histogram 直方图
2) Check sheet 查检表
3) Pareto chart 柏拉图
4) Cause-and-effect diagram 鱼骨图
5) Stratification 层别图
6) Scatter diagram 散点分布图
7) Control chart 控制图
狭义SPC指的就是就是我们常说的控制图 Control Chart,一种对生产过程的关键质量特性值进行测定、记录、评估并监测过程是否处于控制状态的一种图形方法。
控制图除了众所周知的休姆哈特控制图(shewhart control chart)外,其实还有多种其他控制图,如累积和控制图CUSUM(cumulative sum control chart),指数加权移动平均控制图EWMA(Exponentially Weighted Moving-Average control chart)等。本文重点介绍比较常用的休姆哈特控制图。
当我们说到“质量工具”,往往更多地关注了工具的技术层面,而忽略了运用工具的“环境”。这种片面的认知常常导致工具应用的低效。虽然上面提到的7大质量工具是SPC的重要部分,但不能说SPC就是这7大工具,因为SPC还需要一个“持续改善,领导支持”的环境。
如果一个企业没有追求持续改善的文化环境,也没有最高管理层对这种文化环境的追求,那么SPC就不能发挥其威力,这时候SPC就不是真正的SPC了。我想"橘生淮南则为橘,橘生淮北则为枳"大概也就是这个道理。
SPC的发展及应用历史:
最早的控制图是由美国贝尔电话实验室的休姆哈特博士在1924年提出的P图-P Chart,后来此类控制图都被叫做休姆哈特控制图。从休姆哈特的P图算起,SPC理论从创立到今天已接近百年。
SPC理论创立之初,恰逢美国大萧条时期,该理论当时理论无人问津。后来二次世界大战时,SPC理论在帮助美国军方提升武器质量方面大显身手,于是战后开始风行全世界。不过二战后,美国无竞争对手,产品横行天下,SPC在美国并没有得到广泛重视。
日本二战战败后被美国接管,为了帮助日本的战后重建,美国军方邀请戴明到日本讲授SPC理论。1980年日本已居世界质量与劳动生产率的领导地位,其中一个重要的原因就是SPC理论的应用。1984年日本名古屋工业大学调查了115家日本各行业的中小型工厂,结果发现平均每家工厂采用137张控制图。
与SPC相关的几个重要的概念:
(1)变差
就像世界上没有两张完全相同的树叶一样,任何一个工厂,无论其多么先进,从其生产线出来的同一种产品或多或少总会存在一些差异,这种差异就是变差。比如,同一生产线生产出的一批合格螺栓长度不可能做到完全一样。
(2)普通原因 vs 特殊原因
类似于上面螺栓的例子,为什么两个相同的汉堡并不能保证其重量完全相等呢?
这是因为制作汉堡的工艺流程不可能保证每一个汉堡的重量绝对的一样,总会存在一些细微差异。只不过作为顾客我们能够接受这样的差异。我们把导致这种普遍的、固有的、可接受的变差的原因,叫做普通原因 common cause。
但如果哪天你买了两个同样的汉堡,却发现其中一个汉堡中间完全没有添加蔬菜,这不再是常见的、普通的变差,而是有某种特殊原因导致的变差,比如员工的操作的失误。这种变差往往是顾客不能接受的。我们把导致这种非普遍的、非固有的、异常的变差的原因叫做特殊原因 special cause。
你会接受一个漏掉蔬菜的汉堡吗?
(3)受控 vs 不受控
如果一个过程仅仅只有普通原因引起的变差,我们就说这个过程受控 in statistical control;
如果一个过程存在特殊原因引起的变差,我们就说这个过程不受控 out of control。
控制图的使命就是帮助我们发现并消除导致过程变异的特殊原因,这是一个使过程从不受控变成受控的过程。
在这里强调下,过程“受控”不等于“满足设计规范”;“不受控”也不是说就“不满足规范”。受控于是否满足规范是两码事。
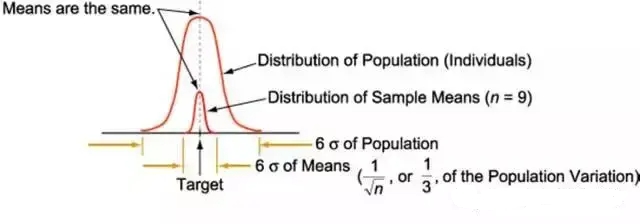
(4)中心极限定理
中心极限定理是SPC的重要理论依据。
这个定理是这样的:
“设X1,X2,...,Xn为n个相互独立同分布随机变量,其总体的分布未知,但其均值和方差都存在,当样本容量足够大时,样本均值的分布将趋近于正态分布”。
如何理解?举个例子:
不管全中国的30岁男人体重成何种分布,我们随机抽N个人的重量并计算其均值,那么当N足够大的时候,那么N个人的平均重量W就会接近于成正态分布。
不禁有人要问多大算“足够大”?记住:如果总体的分布对称,N〉=5时效果就比较理想了;如果总体分布不对称,一般N〉=30时候才算足够大。
这个定理还有一个重要推论:
样本均值的分布将会比总体的分布窄,n是样本容量。
(5)合理的抽样 中心极限定理中我们说到了抽样,那么什么是抽样, 为什么要抽样呢?
抽样(Sampling)就是从研究总体中选取一部分代表性样本的方法。在SPC理论中,抽样是考虑到:
* 经济性,即成本因素;
* 有的质量特性只能进行抽样研究,比如需要通过破坏性实验获得的质量数据。
显然抽样是有风险的,如果抽样不合理,其结果就是“管中窥豹,略见一斑”了,因此我们说要合理抽样(rational sampling)。
合理抽样涉及到几个问题:样本大小、抽样频率、抽样类型(连续取样、随机取样or 其他结构化取样)。
为了满足统计过程控制的目标, 抽样计划必须确保:
* 样本内变差包含了几乎所有由普通原因造成的变差;
* 子组内不存在由特殊原因造成的变差, 即所有特殊原因造成的影响都被限制在样本之间的时间周期上。
抽样大小(子组大小)会影响控制图的敏感度,样本越大能探测到的均值偏移Mean Shift 越小。一般来说,计量型数据推荐最少取4至5个连续零件,计数型数据样本一般不少于500(20~25组,每组至少25个数据)。
2
如何使用SPC控制图
休姆哈特控制图类型介绍
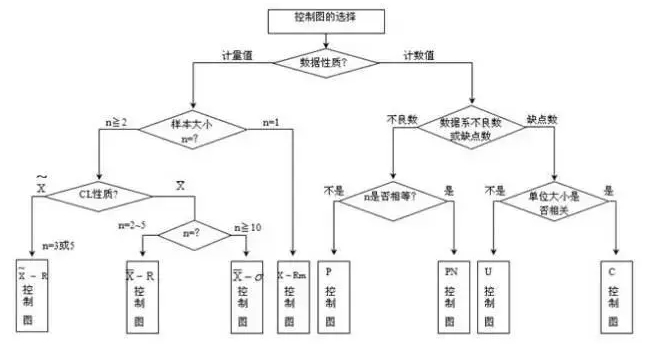
关于SPC控制图的制作步骤,我们来看个流程图:
计量型数值涉及四种控制图:
1. X-Bar & R chart--均值-极差控制图
最常用、最基本的 控制图,控制对象为长大衣、重量、强度、纯度、时间和生产量等计量值的场合。
2. I & MR chart--单值-移动极差图
此图灵敏度较其他三个图差一些,多用于以下场合:
* 自动化检测(对每一个产品都检测);
* 破坏性取样,成本高;
*样品均匀,如化工等过程,多取样也没用。
3. X-Bar & S chart --均值-标准差控制图
与均值-极差图类似,只是用标准差图(S图)代替了极差图(R图)而已;极差计算简便故R图用得广泛,但当样本量n>=9时,应用极差估计总体标准差的效率减低顾最好用S图替代R图。
4. Xmed & R chart--中位数-极差控制图
同样 与均值-极差图类似,只是用中位数图代替了均值图;由于中位数可直接读出非常简单,故多用于现场需要把测定数据直接记入控制图进行管理的场合。
计数型数据,同样涉及四种控制图:
【P】Chart --P控制图
控制对象为不合格品率或合格品率等计数值质量指标的场合。
【np】Chart --np控制图
控制对象为不合格品数,由于计算不合格品率需要进行除法,故在样本大小相等时,此图比较简单。
【c】chart --c控制图
用于控制一部机器、一个部件、一定长度、一定面积或任何一定单位中所出现的缺陷数目,如铸件上的砂眼数,机器设备故障数等。
【u】chart --u控制图
当样品大小变化时应换算成每单位的缺陷数并用u控制图。
控制图制作步骤
上面8种控制图都属于休姆哈特控制图,其中 X-Bar & R chart 和 I & MR chart 是比较常用的两个。但不管是选择哪种图,都按以下步骤进行:
Step 1:根据数据类型和抽样计划确定控制图类型。
Step 2:使用收集的数据计算过程均值和控制限。
Step 3:计算绘图比例并将数据点, 过程均值和控制限绘制在控制图上。
Step 4:查找不受控的点
确定为什么不受控.
纠正过程的问题, 例如抽样计划, 数据收集方式等.
如果已识别出特定原因, 消除该不受控的点并且用增加的额外数据点代替.
重新计算过程均值和控制限.
重新计算比例并将修订后的数据点, 过程均值和控制限绘制在图上.
继续重复抽样过程直到所有必须的点都受控. 这就建立起了正确的过程均值和控制限.
备注:我们把处于上述步骤 Step 4-d 之前的控制图叫做分析用控制图(Phase I ) ;d 之后的控制图叫做控制用控制图 (Phase II). 分析用控制图阶段就是过程参数未知阶段,而控制用控制图阶段则是过程参数已知阶段。
【分析用控制图】
– 分析用控制图主要分析过程是否稳定和受控,是否处于统计的稳定状态和技术的稳定状态,此时分析的数据常为某一时间段的数据,如一个星期或是一个月;控制用控制图的控制限也即由此阶段的分析而得到的,这是分析用控制图的主要任务之一。
【控制用控制图】
当过程达到我们所确定的“统计稳态和技术稳态”后,才能将分析用控制图的控制线延长作为控制用控制图。这种延长的控制线相当于生产立法,便进入日常管理。
控制图制作案例
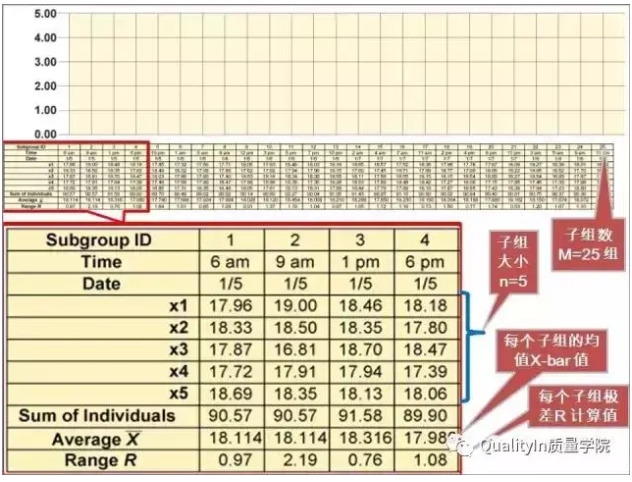
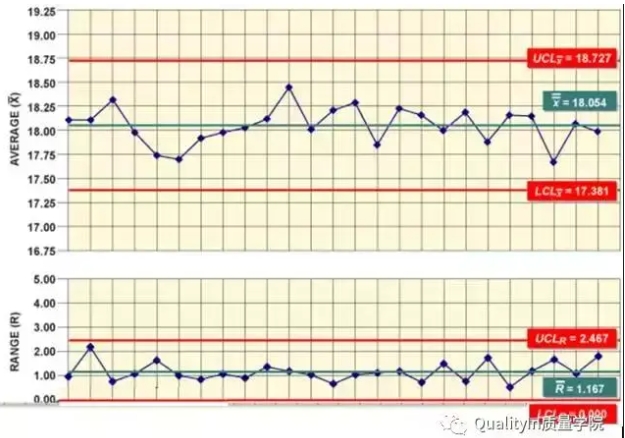
我们将某轴类零件的直径尺寸作SPC监控,假如其Nomial尺寸为18.0mm,按上述4个步骤:
Step1:首先确定控制图类型:变量数据,且容易获取,因此确定选取X-bar & R chart.
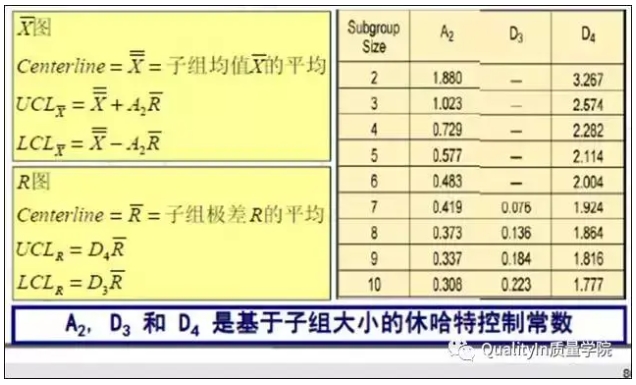
Step2:收集数据,计算初始的均值及控制限。如下表,我们采集了m=25个子组,每个子组大小n=5,共计125个数据。
按如下公式分别可得到X-bar chart, R chart 的上下控制限。
Step 3:开始绘图描点,注意图表刻度比例要合适。
Step4:很幸运,我们没有发现异常点,说明过程本身是稳定和受控的,分析阶段完成,因此我们可将控制限延长开始后续的过程监控。
很多情况下, Step4之前,即“分析阶段” 会出现异常点, 在后续的 “控制阶段”也可能出现异常点,那么如何 “判异” 呢?
控制图判异 在控制图近百年发展中,先后有各种不同类型的判异准则被提出,如:
* Western Electric (WECO) rules
* Nelson Rules
* AIAG Rules
* Juran Rules
....
所以不同的文献资料列举的判异原则可能存在一些差异,我们在选取用哪些判异原则可以根据自己的情况来定。今天我们介绍Minitab中的8大判异准则(结合下图理解):
* 在控制限之外的任何点
* 9 个连续的点在中心线的同一边
* 6 个连续的点连续上升或下降
* 14 个连续的点交互上升和下降
* 3 个点中有2个都在A区或之外
* 5 个点中有4个都在B区或之外
* 15 个连续的点在任一个C区
* 8 个点在C区之外
【原则1】:在控制限之外的任何点
【原则2】:3 个点中有2个都在A区或之外
【原则3】:5 个点中有4个都在B区或之外
【原则4】:连续15个点排列在中心线1个标准差范围内(任一侧)
【原则5】:连续8个点距中心线的距离大于1个标准差(任一侧)
【原则6】:连续9点位于中心线同一侧
【原则7】:连续6点上升或下降
【原则8】:连续14点交替上下变化
其实SPC的内容还可以深入讲很多,除了上面的休姆哈特控制图外,还有累积和控制图CUSUM、指数加权移动平均控制图EWMA等。限于篇幅,SPC控制图应用就介绍到此,希望对大家有一定的帮助。
3
SPC实施中的十大误区 没能找到正确的管制点 不知道哪些点要用管制图进行管制,花费大量的时间与人力在不必要的点上进行管制,殊不知SPC只应用于重点的尺寸(特性的)。
那么重点尺寸/性能如何确定呢?通常应用FMEA的方法,开发重要管制点,严重度为8或以上的点都是考虑的对象(如果客户有指明,依客户要求即可)。
没有适宜的测量工具 计量值管制图需要用测量工具取得管制特性的数值,管制图对测量系统有很高的要求。通常我们要求GR&R不大于10%,而在进行测量系统分析之前,要事先确认测量仪器的分辨力,要求测量仪器具有能够分辨出过程变差的十分之一到五分之一的精度方可用于制程的解析与管制,否则管制图不能识别过程的谈判。
而很多工厂勿略了这一点,导致做出来的管制图没办法有效的应用,甚至造成误导。
没有解析生产过程,直接进行管制 管制图的应用分为两个步骤:解析与管制。在进行制程管制之前一定要进行解析。解析是目的是确定制程是的稳定的,进而是可预测的,并且看过程能力是否符合要求,从而了解到过程是否存在特殊原因、普通原因的变差是否过大等致关重要的制程信息。制程只有在稳定,并且制程能力可以接受的情况下,方才进入管制状态。
解析与管制脱节 在完成制程解析后,如果我们认为制程是稳定且制程能力可接受的,那么,就进入管制状态。制程控制时,是先将管制线画在管制图中,然后依抽样的结果在管制图上进行描点。
那么,管制时管制图的管制线是怎么来的呢?管制图中的管制线是解析得来的,也就是说,过程解析成功后,管制线要延用下去,用于管制。很多工厂没能延用解析得来的管制线,管制图不能表明过程是稳定与受控的。
管制图没有记录重大事项 要知道,管制图所反应的是“过程”的变化。生产的过程输入的要项为5M1E(人、机、料、法、环、量),5M1E的任何变化都可能对生产出来的产品造成影响。换句话说,如果产品的变差过大,那是由5M1E其中的一项或多项变动所引起的。
如果这些变动会引起产品平均值或产品变差较大的变化,那么,这些变化就会在XBAR图或R图上反映出来,我们也就可以从管制图上了解制程的变动。发现有变异就是改善的契机,而改善的第一步就是分析原因,那么,5M1E中的哪些方面发生了变化呢?我们可以查找管制图中记录的重大事项,就可以明了。
所以,在使用控制图的时候,5M1E的任何变化,我们都要记录在管制图中相应的时段上。
不能正确理解XBAR图与R图的含义 当我们把XBAR-R管制图画出来之后,我们到底从图上得哪些有用的资讯呢?这要从XBAR及R图所代表的意义来进行探讨。
首先,这两个图到底先看哪个图?为什么?R反应的是每个子组组内的变差,它反映了在收集数据的这个时间段,制程所发生的变差,所以他代表了组内固有的变差;XBAR图反映的是每个子组的平均值的变化趋势,所以其反映的是组间的变差。
组内变差可以接受时,有明分组是合理的;组间变差没有特殊原因时,表明我们在一段时间内,对过程的管理是有效的、可接受的。所以,我们一般先看R图的趋势,再看XBAR图。
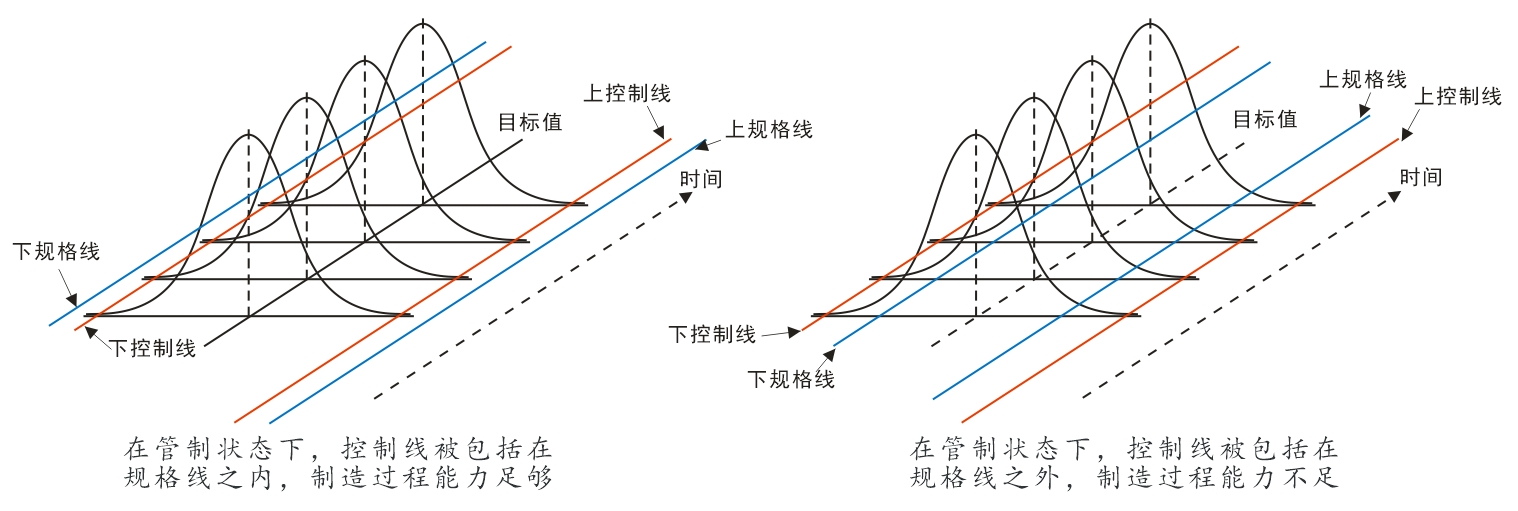
管制线与规格线混为一谈 当产品设计出来之后,规格线就已经定下来了;当产品生产出来后,管制图的管制线也定出来了。规格线是由产品设计者决定的,而管制线是由过程的设计者决定的,管制线是由过程的变差决定的。
管制图上点的变动只能用来判断过程是否稳定受控,与产品规格没有任何的联系,它只决定于生产过程的变差。当西格玛小时,管制线就变得比较窄,反之就变得比较宽,但如果没有特殊原因存在,管制图中的点跑出管制界线的机会只有千分之三。而有些公司在画管制图时,往往画蛇添足,在管制图上再加上上下规格线,并以此来判产品是否合格,这是很没有道理,也是完全没有必要的。
不能正确理解管制图上点变动所代表的意思 我们常常以七点连线来判定制程的异常,也常用超过三分之二的点在C区等法则来判断制程是否出现异常。如果是作业员,只在了解判定准则就好了;但作为品管工程师,如果不理解其中的原委,就没有办法对这些情况作出应变处理。
那么这么判定的理由是什么呢?其实,这些判定法则都是从概率原理作出推论的。比如,我们知道,如果一个产品特性值呈正态分布,那么点落在C区的概率约为4.5%,现在有三分之二的点出现在4.5%的概率区域里,那就与正态分布的原理不一致了,不一致也就是我们所说的异常。
没有将管制图用于改善 大部分公司的管制图都是应客户的要求而建立,所以,最多也只是用于侦测与预防过程特殊原因变异的发生,很少有用于过程改善的。其实,当管制图的点显示有特殊原因出现时,正是过程改善的契机。
如果这个时候我们从异常点切入,能回溯到造成异常发生的5M1E的变化,问题的症结也就找到了。用就管制图进行改善时,往往与分组法、层别法相结全使用,会取得很好的效果。
管制图是品管的事情 SPC 成功的必要条件,是全员培训。每一个人员,都要了解变差、普通原因、特殊原因的观念,与变关有差的人员,都要能看懂管制图,技术人员一定要了解过度调整的概念等。
如果缺乏必要的培训,管制图最终只会被认为是品管人员的事,而其实我们知道,过程的变差及产品的平均值并不由品管决定,变差与平均值更多的是由生产过程设计人员及调机的技术人员所决定的。
如果不了解变差这些观念,大部分人员都会认为:产品只要合符规格就行了!显然,这并不是SPC的意图。所以,只有品管在关注管制图是远远不够的, 我们需要全员对管制图的关注。